Background
jLogo Programming
- Commanding a Turtle
- Pseudocode
- Adding New Commands
- Iteration & Animation
- Hierarchical Structure
- Procedure Inputs
- Operators & Expressions
- Defining Operators
- Words & Sentences
- User Interface Events
- What If? (Predicates)
- Recursion
- Local Variables
- Global Variables
- Word/Sentence Iteration
- Mastermind Project
- Turtles As Actors
- Arrays
- File Input/Output
- AI: Pitcher Problem Solver
Java
- A Java Program
- What's a Class?
- Extending Existing Classes
- Types
- Turtle Graphics
- Control Flow
- User Interface Events
Appendices
- Jargon
- What Is TG?
- TG Directives
- jLogo Primitives
- TG Editor
- Java Tables
- Example Programs
- Installation Notes
Updates
- December 13, 2008
- January 6, 2012
- March 15, 2013
- January 20, 2014
- February 13, 2014
- July 29, 2014
- January 18, 2016
- January 29, 2016
Lastly
Pitcher Problem Solver
Introduction
Artificial intelligence is a hot topic these days. Computer programs have beat chess masters, Go masters, even the best contestants on Jeopardy. But, the study of artificial intelligence goes back a long time.
This project is based on Chapter 14 of Brian Harvey's text, Computer Science, Logo Style, Volume 1: Symbolic Computing. Why did I change Brian's lesson and program?
First, the implementation of Logo used in these lessons does not include some of the advanced features of Berkeley Logo. By substituting more primitive operations, Brian's program can be written in the version of Logo used here.
Second, after I had the program running, I decided to change the main data structure, the tree. I wanted to display the states of all pitchers after each pouring step.
Since the basic design of the program remains the same, I'm copying a lot of text from CSLS, v1. When I do I am including it in a special font, fixed-width, like what follows.
Pitcher Problems
You have probably seen puzzles like this one many times:
You are at the side of a river. You have a three-liter pitcher and
a seven-liter pitcher. The pitchers do not have markings to allow
measuring smaller quantities. You need two liters of water. How can
you measure two liters?
These puzzles are used in some IQ tests, so many people come across
them in schools. To solve the problem, you must pour water from one
pitcher to another. In this particular problem, there are six steps
in the shortest solution:
1. Fill the three-liter pitcher from the river.
2. Pour the three liters from the three-liter pitcher into the
seven-liter pitcher.
3. Fill the three-liter pitcher from the river again.
4. Pour the three liters from the three-liter pitcher into the
seven-liter pitcher (which now contains six liters).
5. Fill the three-liter pitcher from the river yet again.
6. Pour from the three-liter pitcher into the seven-liter
pitcher until the latter is full. This requires one liter,
since the seven-liter pitcher had six liters of water after
step 4. This step leaves two liters in the three-liter
pitcher.
This example is a relatively hard pitcher problem, since it
requires six steps in the solution. On the other hand, it doesn't
require pouring water back into the river, and it doesn't have any
unnecessary pitchers. An actual IQ test has several such problems,
starting with really easy ones like this:
You are at the side of a river. You have a three-liter pitcher
and a seven-liter pitcher. The pitchers do not have markings
to allow measuring smaller quantities. You need four liters
of water. How can you measure four liters?
and progressing to harder ones like this:
You are at the side of a river. You have a two-liter pitcher,
a five-liter pitcher, and a ten-liter pitcher. The pitchers
do not have markings to allow measuring smaller quantities.
You need one liter of water. How can you measure one liter?
The goal of this project is a program that can solve these problems.
Here is a version of the program rewritten in JavaScript so that it can be embedded in this lesson. Try the examples Brian described - enter "3 7" into the box to the right of Available Pitcher Sizes and enter "2" in the box to the right of Desired Amount then click on the Solve Problem button.
| Pitcher Problem Solver |
|---|
The Approach Taken For The Program
How do people solve these problems? Probably you try a variety of special-purpose techniques. For example, you look at the sums and differences of the pitcher sizes to see if you can match the goal that way. In the problem about measuring 4 liters with a 3 liter pitcher and a 7 liter pitcher, you probably recognized right away that 7 - 3 = 4. A more sophisticated approach is to look at the remainders when one pitcher size is divided by another. In the last example, trying to measure 1 liter with pitchers of two, five, and 10 liters, you might notice that the remainder of 5/2 is 1. That means that after removing some number of twos from five, you're left with one.
Brian takes the following few pages to detail how pitcher problems can be solved with algebraic equations, specifically Diophantine equations, before he continues...
My program does not solve pitcher problems by manipulating Diophantine equations. Instead, it simply tries every possible sequence of pouring steps until one of the pitchers contains the desired amount of water. This method is not feasible for a human being, because the number of possible sequences is generally quite large. Computers are better than people at doing large numbers of calculations quickly; people have the almost magical ability to notice the one relevant pattern in a problem without trying all the possibilities. (Some researchers attribute this human ability to "parallel processing" - the fact that the human brain can carry on several independent trains of thought all at once. They are beginning to build computers designed for parallel processing, and hope that these machines will be able to perform more like people than traditional computers.)
What Brian describes above, the approach our program will take, is one of the tactics used by computer scientists exploring artificial intellegence in its earliest days. The program will appear to be intelligent, smart enough to solve the problems quickly. But it will actually take a very simple approach; for each pouring step it will iterate through all possible source-pitcher to destination-pitcher combinations and rely on the incredible speed of a computer to find an answer.
Source-Destination Pairs
Table x.1 shows all of the possible pouring procedures for each step of a two pitcher problem, nine permutations (with repetition allowed) of source-destination pairs. Numbers are used to represent the objects in the problems: zero for the river, one for the first pitcher, two for the second pitcher, etc... Two-number sentences (source-destination pairs) represent the action performed in a pouring step, e.g. [0 1] for filling pitcher 1 from the river, [1 2] for pouring from pitcher 1 into pitcher 2, [2 0] for emptying pitcher 2 into the river, etc...
[0 0] |
[0 1] |
[0 2] |
[1 0] |
[1 1] |
[1 2] |
[2 0] |
[2 1] |
[2 2] |
|
|
||
The code we need to write to generate this list of source-destination pairs involves a Logo primative you haven't seen yet as well as a new kind of data structure. Since we will need these to write our program and I like to get something working as soon as I can, here is code that generates a list of the possible source-destination pairs.
|
And when I invoke genSrcDestPairs I get:
|
There are a couple of things in this code that haven't been covered in the lessons so far.
This is the first time I've taken advantage of Logo's dynamic scope. Notice that both the maxSrcDest and permutations variables are referenced in genPermutationsHelper, but are not global variables; they are local variables in other procedures. maxSrcDest is a local variable (an input) in genPermutations. permutations is declared to be a local variable in genSrcDestPairs. Logo lets procedures access local variables that are declared in the procedure that invoked them, and the procedure that invoked that procedure, etc... Here is a slightly modified paragraph where Brian introduces terms used when explaining dynamic scope.
(A program is a bunch of procedures that work together to achieve
a common goal.) genSrcDestPairs is the top-level procedure. In
other words, genSrcDestPairs is the procedure that you invoke at
the question-mark prompt in the CommandCenter to set the program
in motion. genPermutations is a subprocedure of genSrcDestPairs,
which means that genPermutations is invoked by an instruction
inside genSrcDestPairs. Similarly, genSrcDestPairs is a
superprocedure of genPermutations.
In summary, subprocedures have access to local variables in their superprocedures. So, getPermutationsHelper can access local variables in genPermutations and genPermutations can access local variables in genSrcDestPairs.
I think taking advantage of this feature is usually not a good idea. It makes reading the source code of a program, understanding what is going on, a bit more difficult. You need to know which procedure is invoking and/or being invoked by which procedure. But in this tiny example program it seems like a safe thing to do and makes these procedures easier to understand.
This is also the first time I've demonstrated this kind of list, one used for compound data. The programs in these lessons have been using a special kind of list, a flat list also known as a sentence, for compound data since the Words and Sentences lesson. We've been using sentences not just for printing text but also for data structures, e.g., points/positions in turtle space, a grid cell location - its row and column numbers. But this list is not a list of words, it's a list of lists. And we need a few operators I have not talked about yet to create and manipulate them. Figure x.1 shows the difference between the LIST and SENTENCE operators.

|
Now let me explain the lput operator. To add a member onto the end of a list we can't use the list operator. It would make a new list with its inputs as the members. Figure x.2 shows what we would get (I simply changed lput to list and swapped the inputs).

|
Look at all those square brackets... We created a new list every time a new member was added instead of appending the new member.
fput acts just like lput except the new member is prepended to a list, pushed onto the front of it. Table x.1 summarizes these new operators.
| Operator | Inputs | Description |
| LIST | thing1 thing2 |
Outputs a list whose members are its inputs, which can be any jLogo datum (arrays, lists, and words). |
| (LIST ...) | ... | Outputs a list whose members are inputs up to the closing parenthesis. Members can be any jLogo datum (arrays, lists, and words). |
| FPUT | thing list |
Outputs a list equal to its second input (list) with the first input (thing) prepended, the new first member. |
| LPUT | thing list |
Outputs a list equal to its second input (list) with the first input (thing) appended, the new last member. |
| |
||
Trees
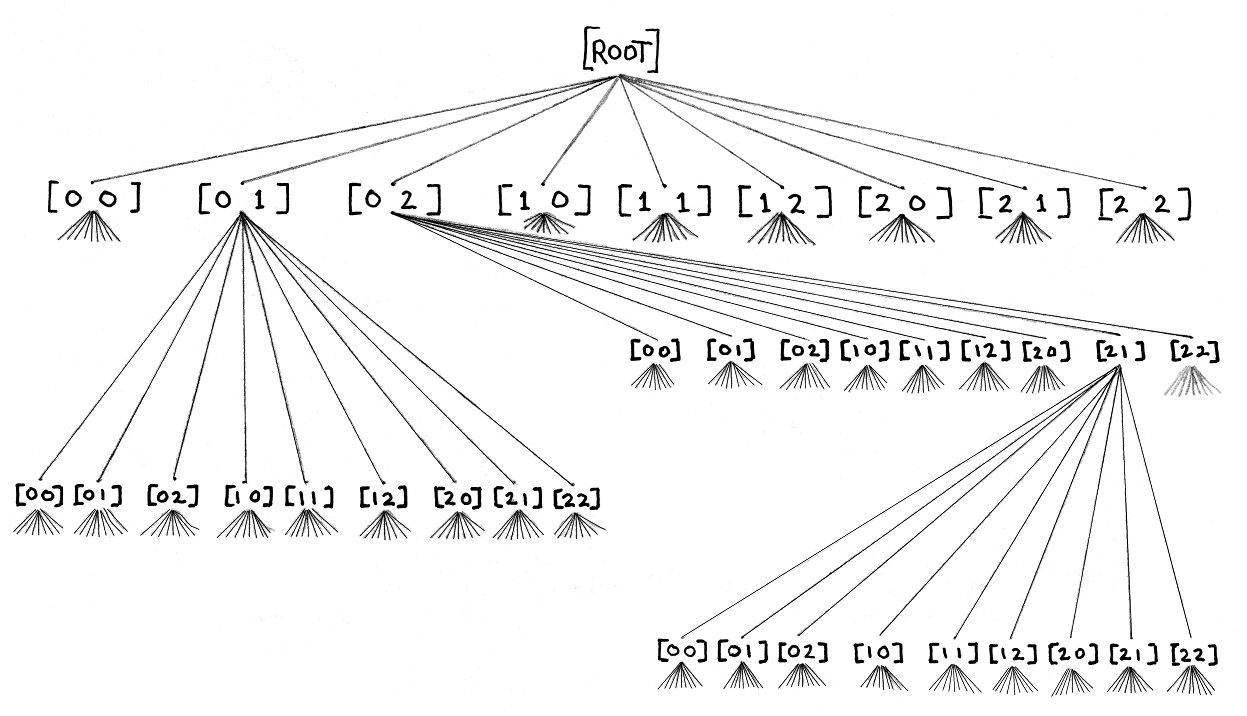
When recursion was introduced in lesson 13, one of the projects was drawing a tree. This lesson involves a tree too. The tree we will use in this program is a mathematical tree. It will be shown upside-down in figures. And, where each branch of trees we drew had two sub-branches, each branch of this new tree will fan out nine child nodes - one for each source-destination pair. Figure x.2 shows a tree for problems involving two pitchers.
|
|
|
Time to explain our tree. We start at the root node where both of the pitchers are empty. Nine paths fan out from the root to level-1 nodes. One for each of the source-destination pair permutations that represent a pouring step. Brian had a similar figure and here is what he had to say.
At each level of the tree, the number of nodes is multiplied by nine. If we're trying to measure two liters of water [given a 3 liter and 7 liter pitcher], a six-step problem, the level of the tree at which the solution is found will have 531,441 nodes! You can see that efficiency will be an important consideration in this program.
So how do we trim our tree to fewer nodes? In figure x.3, for level-1, there are only two meaningful nodes. I have drawn their paths out to level-2 nodes. Our program will ignore the other seven level-1 nodes. Why?
First, three source-destination pairs do not do anything: [0 0], [1 1], and [2 2]. They have the source equal to the destination. So they do nothing. Second, the remaining four pairs do not do anything because the source is an empty pitcher: [1 0], [1 2], [2 0], and [2 1]. Again, our program will ignore pouring steps which pour from an empty pitcher.
The Pouring Data Structure
So we have source-destination pairs organized in a tree structure to let us explore all possible solutions to a pitcher problem. What are we missing? Answer: the amounts of water in the pitchers after each pouring step. We need this so that we can check for a pitcher with the desired amount, the solution to the problem.
I'm naming this combined data a pouring, the source-destination pair combined with the results of a pouring step. The new piece will be called the pitcher states.One possible data structure is a list composed of the source-destination pair (which is a sentence) and a sentence that consists of the amounts of water in each pitcher, the pitcher-states. In this case, here is what the level-1 nodes would look like.
root
[[] [0 0]]
/ \
/ \
[[0 1] [3 0]] [[0 2] [0 7]]
On the bottom-left we have [0 1] for a source-destination pair (river to pitcher one) with results [3 0] - pitcher one is full (3 liters) and pitcher two is empty. On the bottom-right we have [0 2] for a source-destination pair (river to pitcher two) with results [0 7] - pitcher one is empty and pitcher two is full (7 liters).
An alternative, one that Brian took, is a data structure that consists of a list with its first member being the source-destination pair and the rest of the list being the pitcher states, one member for each pitcher. Here is what the level-1 nodes look like in this case.
root
[[] 0 0]
/ \
/ \
[[0 1] 3 0] [[0 2] 0 7]
I chose to go with Brian's list structure. Here are the Logo instructions to access the members of a pouring.
|
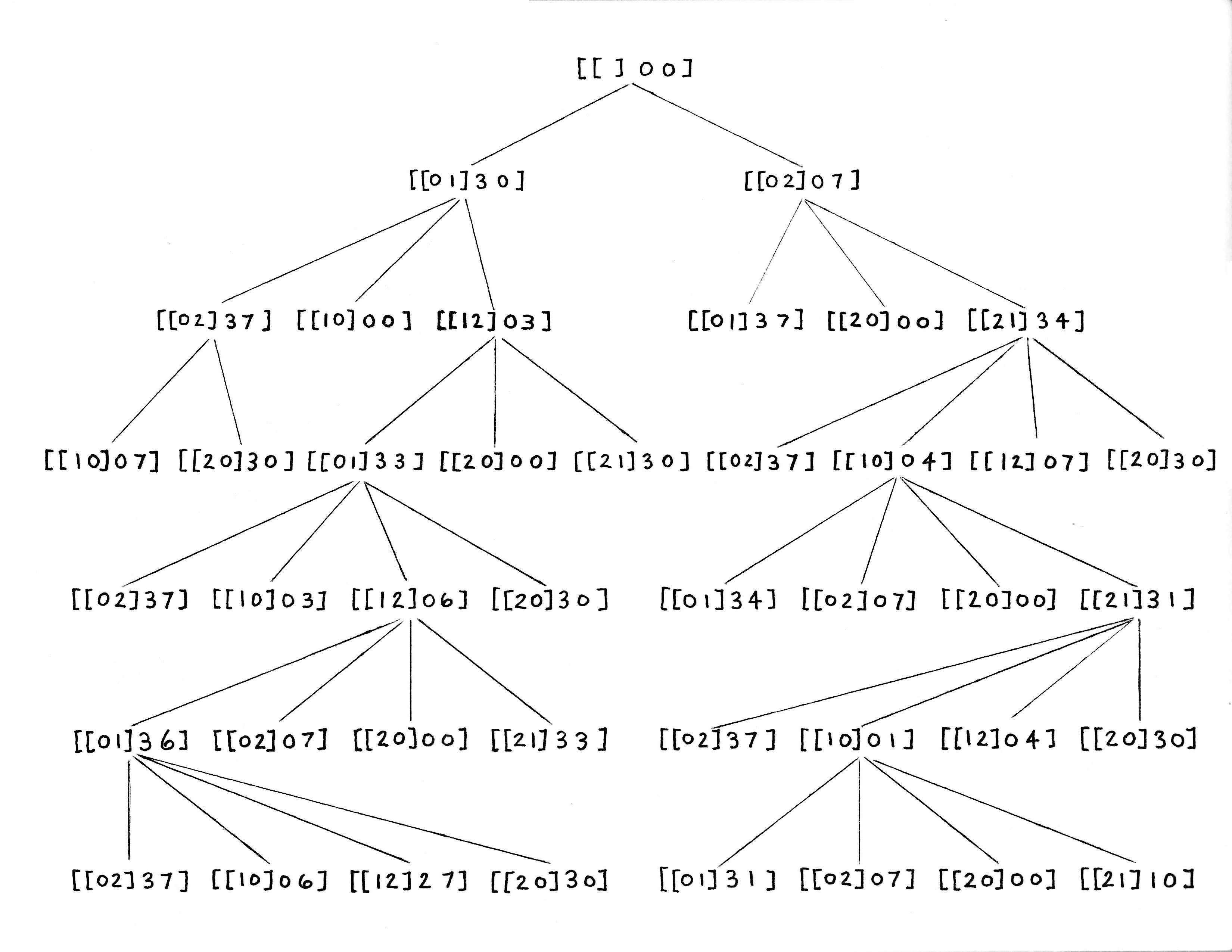
Given this, Figure x.4 shows what our tree looks like now for two pitchers, sizes 3 liters and 7 liters.
|
|
|
As already mentioned, I've eliminated nodes of the tree where the source and destination were equal (nothing achieved) and nodes where the source was an empty pitcher (nothing achieved). I've also eliminated two other "nothing that matters" pouring steps. First, trying to pour into a full pitcher accomplishes nothing. Second, when a pouring step generates a pitchers state that already exists in the tree there is no reason to duplicate what will be the resultant sub-tree.
Before I move on and start writing some code it's time to make sure that we understand our data structures and how we get to solutions. With pitcher sizes three and seven, there are only five sizes that make for good problems. The solutions for three or seven liters is simple, fill the pitcher from the river. That leaves us with one, two, four, five, and six. Let's walk through two and leave the others for you to explore on your own.
The simplest problem to solve is for 4 liters. It only takes two steps: (1) fill pitcher two, the 7 liter pitcher, from the river, (2) fill pitcher one, the 3 liter pitcher, from pitcher two. This leaves 4 liters in pitcher two. Look at Figure x.4 and follow the path down the right side. We go from the root node [[] 0 0] to the first level node [[0 2] 0 7] and on to the second level node [[2 1] 3 4].
More difficult problems... solve for either one or 6 liters. I'll walk through the tree for the solution for six, leave 1 liter to you. First go back to the solver program above and get the solution. Figure x.5 shows the results for our problem.

|
|
|
Now let's walk through the tree, one level down for each pouring step.
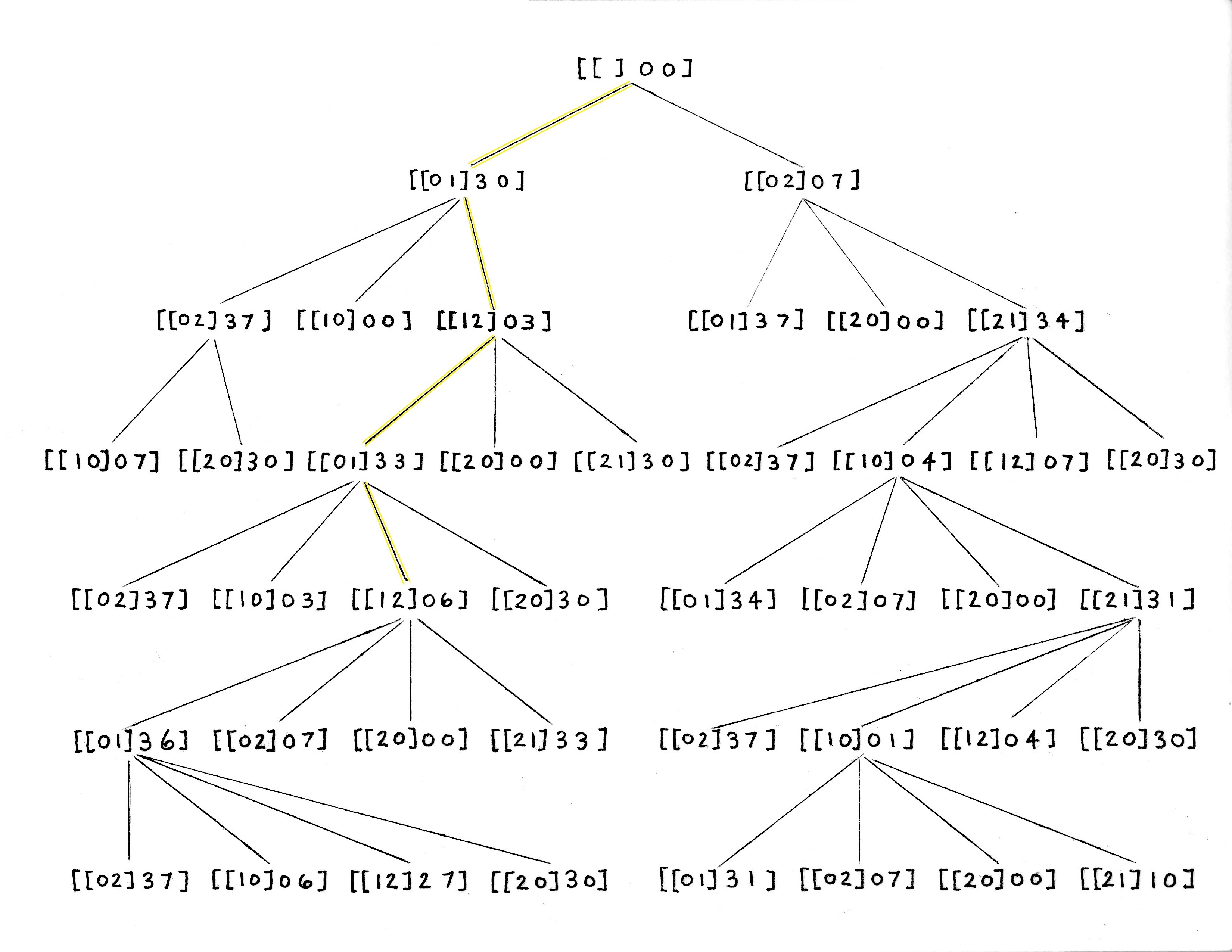
- Coming off the root node with both pitchers empty, fill pitcher one from the river. The pouring data for this level-1 node is [[0 1] 3 0].
- Coming off the level-1 node with pitcher one full and pitcher two empty, fill pitcher two from pitcher one. The pouring data for this node is [[1 2] 0 3].
- Coming off the level-2 node with pitcher one empty and pitcher two containing 3 liters, fill pitcher one from the river. The pouring data for this node is [[0 1] 3 3].
- Coming off the level-3 node with pitcher one full and pitcher two containing 3 liters, fill pitcher two from pitcher one. The pouring data for this node is [[1 2] 0 6].
Figure x.6 shows the tree with this path and concerned nodes highlighted.
|
|
|
Now your turn, walk through the tree to find the first node containing a pouring data structure with a pitcher containing 1 liter. Once you think you have the identified the path through the tree and the involved pouring data structures (nodes in the tree), click here to check your understanding.
Ok... two more desired amount problems, 2 liters and 5 liters. The 2 liter problem can be solved in 6 steps. Walk through the tree to find the first node containing a pouring data structure with a pitcher containing 2 liters. Once you think you have the identified the path through the tree and the involved pouring data structures (nodes in the tree), click here to check your understanding.
And this leaves solving for 5 liters. Well, this solution takes 8 steps and I didn't have large enough graph paper to draw 8 levels, 8 steps. As an advanced exercise... draw the path through the first 6 levels and then draw the last three levels, the nodes, and path along the solution. Click here to check your solution.
Code For Creating/Walking Our Tree
Now that we have a data structure that we have used to manually solve pitcher problems, it is time to write a Logo program to do the same. As I did when I drew the trees, and you did if you completed the tree for a solution for 5 liters, we did this in a few steps. As I drew each level based on the level above it, I went through the source-destination pairs for each node in my head, eliminating pourings that wouldn't help get me to the solution. I went down the page and left-to-right across it. This was equivalent to what is called breadth-first search in computer science speak. Here is a bit of background on tree searches from Brian.
In some projects, a tree is represented within the program by a Logo list. That's not going to be the case in this project. The tree is not explicitly represented in the program at all, although the program will maintain a list of the particular nodes of the tree that are under consideration at a given moment. The entire tree can't be represented as a list because it's infinitely deep! In this project, the tree diagram is just something that should be in your mind as a model of what the program is doing: it's searching through the tree, looking for a node that includes the goal quantity as one of its numbers. Depth-first and Breadth-first Searching Many programming problems can be represented as searches through trees. For example, a chess-playing program has to search through a tree of moves. The root of the tree is the initial board position; the second level of the tree contains the possible first moves by white; the third level contains the possible responses by black to each possible move by white; and so on. There are two general techniques for searching a tree. These techniques are called depth-first search and breadth-first search and In the first technique, the program explores all of the "descendents" of a given node before looking at the "siblings" of that node. In the chess example, a depth-first search would mean that the program would explore all the possible outcomes (continuing to the end of the game) of a particular opening move, then go on to do the same for another opening move. In breadth-first search, the program examines all the nodes at a given level of the tree, then goes on to generate and examine the nodes at the next level. Which technique is more appropriate will depend on the nature of the problem.
Given this, it is obvious that solving pitcher problems will be an exercise in a breadth-first search. We want to find a solution that takes the fewest number of steps, looking at nodes in the fewest levels of the tree as possible. Here is the tree walking code.
; Tree Walking Stuff
; ---- ------- -----
; Two algorithms are provided which iterate through all nodes of a
; tree: depthFirst and breadthFirst.
;
; Each of these procedures expects two procedures to exist
;
; (1) processNode - invoked for every node of the tree
; one input, a node
;
; (2) childNodes - invoked to get a list of child nodes for a node
; one input, a node
...
; perform a breadthFirst traversal of a tree
; the procedure processNode is invoked for each node in the tree
; the function childNodes, which has one input :node, should output
; a list of the :node's children
; :node should contain the root node of the tree
to breadthFirst :node
breadthFirstHelper (list :node)
end
; :queue is a list of nodes to be processed
; for every member of the queue, from first to last, the first
; node from :queue is passed to two procedures (processNode
; and childNodes) as an input.
; processNode checks to see if its input :node, a pouring data
; structure, has a pitcher with the desired amount. If so,
; global variable solution is set to the node.
; childNodes outputs a list of nodes that are children of the
; input node. These nodes are appended to :queue to be
; processed later.
to breadthFirstHelper :queue
if empty? :queue [stop]
processNode first :queue
if not empty? :solution [stop]
breadthFirstHelperHelper (childNodes first :queue)
breadthFirstHelper butfirst :queue
end
; Append the new child nodes onto :queue
to breadthFirstHelperHelper :childNodeList
if empty? :childNodeList [stop]
make "queue lput (first :childNodeList) :queue
end
breadthFirstHelper is a straight-forward recursive procedure. It processes tree nodes in a top-down, left-right manner (breadth-first) due to the way nodes are added to queue. After each node is processed, its children (part of the next level of the tree) are added to the end of queue.
breadthFirstHelperHelper does the work of appending the child nodes. Two things you should notice, understand. One, it uses LPUT to append child nodes onto queue. Two, this is the first time I've taken advantage of Logo's dynamic scope. Notice that :queue is referenced but it is not a global variable. It is a local variable (an input) to breadthFirstHelper. Logo lets procedures access variables that are accessable in the procedure that invoked them. I think taking advantage of this feature is not usually a good idea. But in this example it seems like a safe thing to do and makes these procedures easier to understand.
The above code was not my first solution. Here is that code. Check it out; compare how it generate the same results. A big part of programming is rewriting stuff when you understand it better.
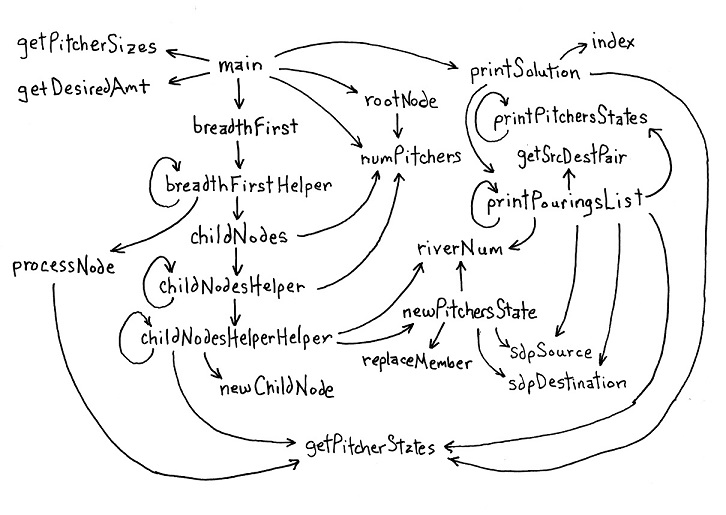
Here is the full program as it currently stands, just so you can see the big picture. It also contains the framework for the complete program including a main procedure and initialization. You can copy/paste it into TG; it will run, but does nothing.
processNode and childNodes Procedures
The processNode procedure is simple. It is a single IF instruction that checks to see if the the solution value matches any of this node's (this pouring's) pitchers states. If so, solution, a global variable, is set to this node. Notice that I have a commented-out a print instruction. It will be used while testing the program.
; Check :node to see if one of the pitchers has the desired amount
; If found, set the global variable "solution to the node
to processNode :node
;print "|processNode | show :node
if member? :desiredAmount (getPitcherStates :node) [make "solution :node]
end
On the other hand, childNodes and its subprocedures consist of most of the complexity in the program. The start of what is needed is the genSrcDestPairs program from the beginning of this lesson. I copy/pasted this into the program and renamed the genSrcDestPairs procedure childNodes and changed genPermutations to childNodesHelper. These procedures are almost identical except for renaming stuff. The new childNodes procedure outputs a list of pourings instead of printing out the generated list.
This left the procedure genPermutationsHelper which I renamed childNodesHelperHelper. Instead of appending a source-destination pair to the list being assembled, the body of this procedure was changed to build a pouring and append this to the list being assembled. Here is the code for it.
; iterate through all possible destination numbers. for each, compute ; the new pitcher states for the source-destination pair and combine ; them to form a new pouring. Append the new pouring onto childNodeList to childNodesHelperHelper :dest if greater? :dest :maxSrcDest [stop] localmake "curStates getPitcherStates :node localmake "newSrcDestPair sentence :src :dest localmake "newState newPitcherStates :curStates :newSrcDestPair localmake "pouring fput :newSrcDestPair :newState make "childNodeList lput :pouring :childNodeList childNodesHelperHelper (+ :dest 1) end
To complete construction of a pouring, a list of new pitcher states, that result from the source to destination transfer of water, needs to be computed. This is the purpose of the procedure newPitcherStates which is passed two inputs, the current states of pitchers and a source-destination pair. The procedure computes new states with five rules, IF instructions. The first is obvious, if the source is the same as the destination nothing happens so output the existing states. The next two rules involve the river as a source and a destination. These are also simple, a pitcher is either filled or emptied. The final two rules deal with pitcher-to-pitcher transfers with the difference being whether or not all of the contents of the source will fit into the destination. Here is code for it.
; Output a new sentence of pitcher-states (volumes) given an existing
; pitcher-states sentence and a source-destination pair for a new pouring
to newPitcherStates :existingStates :srcDestPair
localmake "dest sdpDestination :srcDestPair
localmake "src sdpSource :srcDestPair
if equal? :src :dest [output :existingStates]
; if destination is river, source is now empty
if equal? :dest riverNum [output replaceMember :existingStates :src 0]
; if source is river, destination (which must be a pitcher) is now full
localmake "destPitcherCapacity (item :dest :pitcherSizes)
if equal? :src riverNum ~
[output replaceMember :existingStates :dest :destPitcherCapacity]
; pouring is pitcher to pitcher so the state of both will change
localmake "srcPitcherVolume (item :src :existingStates)
localmake "destPitcherVolume (item :dest :existingStates)
localmake "destPitcherAvailSpace (- :destPitcherCapacity :destPitcherVolume)
; if destination pitcher has room for the contents of the source pitcher,
; empty source into destination
if lessequal? :srcPitcherVolume :destPitcherAvailSpace ~
[localmake "newStates replaceMember :existingStates ~
:dest ~
(+ :destPitcherVolume :srcPitcherVolume) ~
output replaceMember :newStates :src 0]
; destination pitcher has room for some of the source pitcher's water, but not all
localmake "newStates replaceMember :existingStates ~
:src ~
(- :srcPitcherVolume :destPitcherAvailSpace)
output replaceMember :newStates :dest :destPitcherCapacity
end
To be continued
This is an incomplete lesson - just the beginning. I think Brian rewrote his version of the program multiple times. I have rewritten it three times. If you complete it on your own another way and think it's an improvement, send it to me please.
When drawing figure x.y i added a SHOW to xxx to display seenPitcherStates, to make sure my followed paths through the tree were along the lines on newly discovered pitcher states. i noticed something interesting. even after a solution was discovered (level 4, [[1 2] 0 6]) another new pitcher states was found to the right on level 4, [[2 1] 3 1]. i thought that the algorithm would quit processing members of the queue once a solution was found. not so, the algorithm only terminated when all members of the current level were processed. so, it shows that viewing the data in your programs can point out execution that is unexpected, not what one thought was happening.
until we get to writing the printSolution procedure, tree nodes are simply pouring data structures, so that is what rootNode produces. once we switch to tree nodes being lists of pouring data structures, rootNode will need to output a list of a single initial pouring. processNode will need to get the last pouring from the node to extract its pitcher states. childNodeHelperHelper references to :node need to become (last :node) and near the end of the procedure, newChildNode changes.
current discussion on SIGCSE includes importance of static type checking for introductory programming courses. i just had this idea... as long as access to data is abstracted to creator/getter/setter procedures, a type could be prepended and checked. example: a srcDestPair could be maintained as [srcDestPair [# #]] and the type verified before access/manipulation. It's not static but it will detect bugs at runtime.
|
|
|