Background

• Preface
• Table of Contents
• What's Computer Programming?

jLogo Programming

• Commanding a Turtle
• Pseudocode
• Adding New Commands
• Iteration & Animation
• Hierarchical Structure
• Procedure Inputs
• Operators & Expressions
• Defining Operators
• Words & Sentences
• User Interface Events
• What If? (Predicates)
• Recursion
• Local Variables
• Global Variables
• Word/Sentence Iteration
• Mastermind Project
• Turtles As Actors
• Arrays
• File Input/Output
• AI: Pitcher Problem Solver

Java

• A Java Program
• What's a Class?
• Extending Existing Classes
• Types
• Turtle Graphics
• Control Flow
• User Interface Events

Appendices

• Jargon
• What Is TG?
• TG Directives
• jLogo Primitives
• TG Editor
• Java Tables
• Example Programs
• Installation Notes

Updates

• December 13, 2008
• March 7, 2009
• January 6, 2012
• March 15, 2013
• January 20, 2014
• February 13, 2014
• July 29, 2014
• January 18, 2016
• January 29, 2016

Lastly

• Acknowledgements
• About Me

Procedure Inputs

Introduction

Hopefully by now I've convinced you that programming involves a process of solving problems in stages.  Since most computer programs that you will want to write are too complex to simply type-in, you need to take advantage of the concept of procedural abstraction.  Break the problem that you are writing into pieces.  Think about what you need to do; of this, think about what you already know how to do.

Start writing a program in pieces.  Each piece is written as a procedure which you define.  Your procedures are simply lists of instructions.  In techie terms, you are using abstraction to make the source code easier to understand and thus easier to write correctly and easier to enhance.

As you think about the steps or as you are typing in instructions, you will recognize similarities or patterns in the code.  When you discover a pattern with the same instructions being used over and over again, you can reduce the amount of source code you have to type by using iteration - you learned about this (the repeat command) a couple of lessons ago. Using iteration makes your programs smaller, and so, easier to understand.

But, iteration only lets you eliminate duplicated instructions, identical source code, that your want to do multiple times.

In this lesson, you will learn how to define procedures that have inputs, also known as parameters.  These inputs (their names) are used in the body of the procedure in place of specific (actual) values.  When you invoke the procedure, you provide a specific (actual) value to use in place of the input, everywhere its name is in the body of the procedure.

Procedures with inputs allow you to reduce multiple, similar, patterns of instruction sequences to a single instruction.  Confused?  It will become clearer as this lesson progresses...

Similar, But Different, Boxes

Look at the series of objects in Figure 7.1.  What are the similarities of the objects?  What are the differences?  Take a moment to write your thoughts.

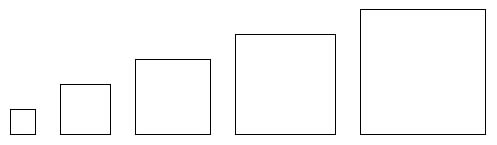Figure 7.1

Now, write a program, boxes, which draws the series of growing boxes.  Your program should consist of a procedure for each box.  Then, write a main procedure which contains invocations of these new procedures.  Finally, invoke main to display the row of boxes.

If you are confused, refresh your memory regarding defining procedures, review Definition of a Procedure.  Also rereading the last lesson's Summary may help.  Give this exercise a good effort before reading on.

Similar Procedures

Here are my definitions of the procedures which draw the first couple of boxes and part of the definition of the main procedure.

   ;draw a box 25 turtle steps on a side
   to box25
     repeat 4 [forward 25 right 90]
     end

   ;draw a box 50 turtle steps on a side
   to box50
     repeat 4 [forward 50 right 90]
     end

   to main
     home clean setheading 0 setpencolor 0 setpensize 1   
     penup left 90 forward 250 right 90 pendown
     box25
     penup right 90 forward 70 left 90 pendown
     box50
     ;...
     end 

Since the procedures draw different sized boxes, I've given each of them an appropriate name.  But check them out carefully, the only difference in the instructions that make-up the bodies of these procedures is the number of steps that the turtle is told to move forward.

Think about this scenario.  Logo doesn't have an infinite set of forward commands, e.g., fd25, fd50, fd75, etc...  There are not commands for all possible right instructions, e.g., rt30, rt45, rt90, etc...  There are commands forward, fd, right, and rt which expect an input that specifies the number of steps to move or the number of degrees to rotate.

We obviously need the capability to define procedures that can be used in a similar manner.  We need the ability to define a procedure named box that expects to get a number when it's invoked.  The number will determine the size of the box drawn.

What we need is called an input.

Defining a Procedure With an Input

Here is what we want...

   ;draw a box of a specified size.
   to box :size
     repeat 4 [forward :size right 90]   
     end 

This procedure definition has an input.  Similar to the way you name the procedure itself, you give the input a name, an identifier.  In this example, I've chosen the name size.  The colon (":") preceding the name (pronounced "dots") tells the interpreter that this word is an input and that it should use what's in it. 

What do I mean, in it?  Well, an input is one kind of a thing that's called a variable.  Variables are containers.  Inputs get a value put into them when the procedure they are part of is invoked.

Up until now, all of the programs you've written have been composed of commands with literals as arguments.  Literals are constants like the number "4" in the repeat instruction in the example above.  Every time box is invoked, the <list-of-Instructions> input to the repeat command is performed 4 times. 

But now, the input to the forward command is a variable - the input named size.  The number of steps that the turtle moves forward is equal to the input provided in an invocation of box.  The turtle moves a variable number of steps every time the Logo interpreter performs the box procedure.

Here's the TG applet.  Type in the example definition of box from above and then invoke it a couple of time with different values as arguments, e.g.,

   box 10   
   box 25
   box 100 

Your browser does not support Java applets. Click here for more information. TG Programming Environment Applet

Then, see what the following repeat instructions do.

   repeat 4 [ box 25 box 50 box 75 left 90 ]    

   repeat 24 [ box 60 box 90 right 15 ] 

Multiple Inputs

Procedures are not limited to zero or one inputs.  Procedures are allowed to have more than one input.  The repeat command we have been using has two, a count and an instruction-list.  Another Logo command that takes two inputs and that we will use later in this lesson is setxy. Its two inputs are an X coordinate followed by a Y coordinate.  The turtle moves in a straight line to the X,Y point, without changing its heading.  If the pen is down, it draws a line to the point.

Here is a list of instructions that draws a triangle in the center of the graphics canvas.

   home clean showturtle throttle 1200
   penup setxy 0 100
   pendown setxy 100 -100  setxy -100 -100 setxy 0 100 

The boxes we have been drawing are squares, a special case of a rectangle.  Here is the definition of a new procedure which draws a rectangle.

   ;draw a rectangle of a specified size, at the turtle's
   ;current location, with current pen size and color
   to drawRectangle :width :height
     repeat 2 [forward :height right 90 forward :width right 90]   
     end 

Type it in.  Try it out.  Play with a variety of different inputs.

Logo Animation - Watching Inputs in Action

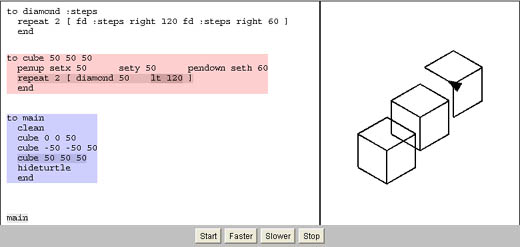Figure 7.2

Click here to see an applet that demonstrates the execution of a small program which draws three cubes.  If you are having any trouble visualizing how inputs get their values when a procedure, which has, them gets invoked, go watch it...  Watch how the program is executed, step by step.

Practice: Cartesian Axes

One thing we have been doing since we started to write our programs is figuring out where we should draw things on the graphics canvas.  What can help with this is to draw a pair of X and Y axes.  They give you guidelines for the center of the canvas, the dividing lines between positive and negative X and Y values.  Tick marks along the the axes help approximate the values of point coordinates, where we draw things.

If you need to learn a bit, or refresh your memory, about the Cartesian coordinate system, here is a link to the Math is Fun website which has a nice page describing it.

Now, let's generalize the program you have seen twice in the exercises, first in the second lesson and also in lesson 5 (Iteration).  Figure 7.3a shows one example of a set axes our program will draw.  Figure 7.3b shows the call graph for the program I have in mind.

(a)  Cartesian Axes	(b)  DrawAxes Call Graph

Figure 7.3

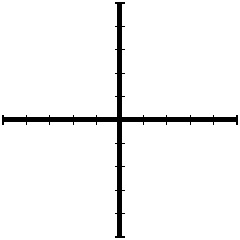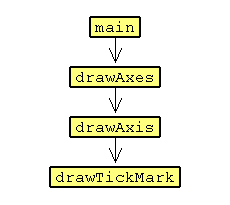Let's start with the code for drawTickMark.

   ; draw a tick mark at the turtle's current location
   ; the tick mark is drawn perpendicular to its heading   
   ; input :len is length the tick mark extends outward
   to drawTickMark :len
     setpensize 1  setpencolor 15
     right 90 forward :len back :len
     left 180 forward :len back :len
     right 90
     end 

And the code for drawAxis which invokes drawTickMark.

   ; draw an axis at the turtle's current location
   ; the axis runs along the turtle's current heading
   ; input :numTicks is the number of tick marks drawn out from the origin
   ; input :gapLen is the distance between tick marks
   ; input :ticLen is the distance a tick mark extends outward from axis
   to drawAxis :numTicks :gapLen :ticLen
     pendown
     repeat :numTicks [setpencolor 0 setpensize 3 forward :gapLen drawTickmark :ticLen]
     penup repeat :numTicks [back :gapLen]
     right 180
     pendown
     repeat :numTicks [setpencolor 0 setpensize 3 forward :gapLen drawTickmark :ticLen]
     penup repeat :numTicks [back :gapLen]
     left 180
     end 

Study these procedures for a few minutes.  If you have TG running on your system, copy/paste them into the Editor.  Or, use the TG applet; the above code is available as DrawAxis.jlogo (use the loadcode directive to get the code into the Editor).

Experiment with drawAxis.

Then write procedures drawAxes and main so that your program draws axes matching those in Figure 7.3(a).

With my solution, I was able to change three numbers in the source code and draw the grid shown in Figure 7.4.  Can you get your program to draw a grid with minimal changes?

Figure 7.4

As you should now be able to see, inputs are a very powerful tool in programming.

Practice: drawRect and fillRect

drawRect

The TG application/applet you are using is written in Java - which is why I've given the dialect of Logo it provides the name jLogo.  One goal is to prepare students for the AP Computer Science curriculum, which currently is based on the Java programming language.  I'm going to take advantage of the current lesson's objective (to introduce procedure inputs) and introduce you to a couple of Java's primitive graphics procedures.  We will then define them as Logo procedures for use in our programs.  Here is a description of the first one, Java's Graphics.drawRect.

    drawRect( int x, int y, int width, int height )

    drawRect draws the outline of the specified rectangle. The
    left and right edges of the rectangle are at x and x + width.
    The top and bottom edges are at y and y + height. The
    rectangle is drawn using the current color.

    Parameters:
    x - the x coordinate of the rectangle to be drawn.
    y - the y coordinate to the rectangle to be drawn.
    width - the width of the rectangle to be drawn.
    height - the height of the rectangle to be drawn.
			

So what are the differences between what we have been doing with the turtle to draw boxes and Java's drawRect procedure?

• Java's Graphics support has no concept of a current location; in Logo it's the turtle's location.  We have been writing procedures that draw things starting whereever the turtle is.  With no current location, Java's drawRect needs to have two inputs, X and Y, which identify the upper-left corner of the rectangle to be drawn.  Why the upper-left corner...
• There is a major difference in the layout of Java's coordinate system when compared with TurtleSpace.  All graphics in Java is relative to the top-left corner of its canvas.  This point is addressed 0,0.  X coordinates increase to the right; Y coordinates increase downwards.  Its coordinates are Whole Numbers.  TurtleSpace is a traditional Cartesian coordinate system, with approximated Real Numbers for coordinates.
• All of the boxes (and polygons) we have drawn so far have been oriented in the direction the turtle is currently headed.  We have had the turtle doing the drawing by moving forward and turning at corners.  This allowed us to draw some very elaborate graphics with simple instructions (see Nested Iteration).  Since Java's Graphics support has no turtle, there is no current heading.  Instead, the edges of the rectangle are parallel with the X and Y axes.
• The rectangular outline produced by Java's drawRect is one pixel wide.  Java's low-level Graphics does not support the concept of a current line thickness.

Taking all of this into account, here is a Logo version of Java's drawRect.

   ;draw a rectangle given its dimensions and location
   ;its sides are oriented north-south and east-west
   ;the turtle's current pen width and color are used
   to drawRect :leftX :bottomY :width :height
     penup  setxy :leftX :bottomY  pendown  setheading 0
     repeat 2 [forward :height right 90 forward :width right 90]   
     end

Read over this code closely.  You'll find the new command introduced above.  setxy moves the turtle to the point in TurtleSpace specified by its two inputs. There are also two other related commands I'll mention now which you should be aware of. setx and sety move the turtle to a provided coordinate, but only in a horizontal or vertical direction (respectively).

Practice: Rewrite boxes

Your turn to write some code; rewrite the boxes program this lesson started off with, naming it DrawBoxes.  Include drawRect in the program and use it (invoke it) to draw all of the boxes.

fillRect

A second Java primitive graphics procedure we will look at and write is fillRect.  Here is a description of it.

    fillRect( int x, int y, int width, int height )

    fillRect fills the specified rectangle. The left and right
    edges of the rectangle are at x and x + width - 1. The top and
    bottom edges are at y and y + height - 1. The resulting rectangle
    covers an area width pixels wide by height pixels tall. The
    rectangle is filled using the graphics context's current color.

    Parameters:
    x - the x coordinate of the rectangle to be filled.
    y - the y coordinate to the rectangle to be filled.
    width - the width of the rectangle to be filled.
    height - the height of the rectangle to be filled.
			

As with our Logo drawRect, we will stick with the X and Y coordinates being the lower-left corner of the filled rectangle.

   ; draw a solid rectangle given its dimensions and location
   ; its sides are oriented north-south and east-west
   ; the rectangle is painted with the current pen color
   to fillRect :leftX :bottomY :width :height
     penup  setxy :leftX :bottomY setheading 0 setpensize 1
     repeat :width [pendown forward :height penup back :height right 90 forward 1 left 90]
     right 90 back :width left 90
     end

Poor turtle... Our fillRect procedure makes it paint all of the pixels one at a time, walking back and forth, back and forth.  But don't worry; as soon as we learn how to do a little math, we will be able to fix this.  I will show you a better fillRect procedure in the operators and expressions lesson.

Practice: Modify DrawBoxes

Your turn to write some code; modify your DrawBoxes program to use fillRect in place of or in addition to drawRect.

Figure 7.5 shows what I came up with; just an example...

Figure 7.5

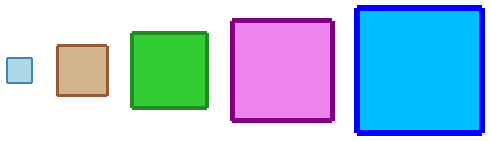Timeout... Does this make sense?

If defining and invoking procedures which have inputs is even the least bit confusing, before moving on, check out the way procedure definition with an input is explained in the book: "Thinking About [TLC] Logo" by clicking on this link.

Projects: Pick One

It is time for you to draw something with a program that uses programming techniques we have learned so far.  In a previous lesson ( Iteration), you learned two ways to draw a circle and how to draw a simple arc.  You've learned the importance of hierarchy for structuring your programs.  And now you know how to write procedures that have inputs - they can do the same sort of thing, but their final result is dependent upon the inputs.

Pick something simple to draw and write a program to draw it. 

Here are a few things I've come up with.  A seascape made entirely using arcs, a custom wheel, and a kitty cat...

Figure 7.6

Summary

In this lesson, you've learned how to extend the utility of procedures.  You now know how to write procedures that can act differently; exactly what gets done depends upon the inputs ( parameters) that are provided on invocations.  This is good for two reasons:

1. You can reduce the size of your programs.  The shorter your programs are, the easier they are to read and understand, the less chance they have mistakes in them, and the less you have to type.
2. Your abstractions can be more powerful.  Without inputs, a procedure does the same thing every time it is invoked.  This is pretty limiting.  But, with inputs, your procedures are much more flexible.