BFOIT - Introduction to Computer Programming

Global Variables

Introduction

What if you need a variable that holds it's value across procedure boundaries, a lifetime that's longer than the execution of a single procedure?

In this lesson, you will learn about a new kind of variable that is declared outside of procedure definitions.  In computer science jargon, the accessibility of a variable (where it's contents can be accessed or changed) is called the scope of the variable.

Think about how a simple calculator works.  You are going to be creating a virtual one later in this lesson.  You will need a variable that holds the current number as it is entered - one digit at a time, one mouse click at a time.  Since the mouseClicked procedure will be executed multiple times - once per digit clicked on, the variable needs to be declared independent of this procedure.  If you are confused by this or if it is just too hard to imagine, play a bit with the calculator applet which appears later in this lesson.  While you do this, think about what needs to be done as numbers are entered, as math keys are clicked on. 

Global Variables

Here is a list of the attributes of global variables.  Global variables

  • are containers whose contents can be accessed anywhere in a program,
  • are declared with the global command,
  • get assigned a value when a make command is interpreted, and
  • maintain a value until changed with another make command.

For your programs, it is best to put your global variable declarations at the top/beginning.  This way, you can see, in one place, the names of variables that will be referenced across procedure boundaries.  Since a declaration creates an empty container, you need to use a make command to put an initial value into it.  Since all programs should have an main procedure that does initialization, this is the best place to put these make instructions.

Use of Global Variables as Symbolic Constants

Let's look at an example of how you can use global variables...

In the lesson Defining Your Own Operators, the first thing I showed you how to do was write procedures that did nothing but output a number.  This is a form of abstraction, where I give names (that mean something to me) to numbers used inside the computer to represent colors.

In all programs written since this lesson, I have defined procedures like black, blue, etc... that simply output the colors' numbers.  Then, using these procedures as an input to a setpencolor command made reading the code easier to understand.  As an example: 

   to red
     output 4
     end

   setpencolor red   

Global variables can be used to achieve the same results.  Here is most of a program (which simulates a progress bar) that shows the use of global variables as symbolic constants.  I left out the bodies of drawRect and fillRect to save space; they are available back in the lesson on predicates if you don't have them handy. 

   global "black make "black 0
   global "blue  make "blue  1

   global "barX  make "barX -100
   global "barY  make "barY 25
   global "barHeight make "barHeight 50
   global "barWidth  make "barWidth 200

   global "amtX  make "amtX sum :barX 2
   global "amtY  make "amtY difference :barY 2
   global "amtHeight make "amtHeight difference :barHeight 4
   global "amtMaxWid make "amtMaxWid difference :barWidth 4

   ; see: http://www.bfoit.org/itp/Predicates.html#rect_procs
   ; for drawRect and fillRect, and east and south which they use

   to updateBar :percent
     localmake "amtWidth product :percent (quotient :amtMaxWid 100)   
     fillRect :amtX :amtY :amtWidth :amtHeight
     end

   to randomDelay
     wait sum 200 (product 100 random 9)
     end

   to main
     hideturtle clean
     setpensize 2 setpencolor :black
     drawRect :barX :barY :barWidth :barHeight
     setpencolor :blue
     repeat 50 [updateBar (product repcount 2) randomDelay]
     end

   main

So, what's going on here?  Well, as soon as a global instruction is interpreted, an empty variable is created.  The name of this variable is available anywhere in the program, following this declaration.  This is the reason that the first thing that you should do in a program is to declare all of the global variables in it.

The syntax of the global command is:

   global       <name>  

  1. the command name: global and
  2. <name>, a word, the variable's identifier

Here is the TG applet.  Play around a bit.  Declare a few global variables, try accessing them before you use a make command to give them their initial values, use make to set their initial values, and then access them.  Write a procedure which has inputs (e.g. boxAt :x :y :size) and notice that once you type in the end word which terminates your definition of boxAt, you can no longer reference its inputs.  Type in the example I gave above to see what it does, make sure you understand it.

Your browser does not support Java applets. Click here for more information. TG Programming Environment Applet

The use of names in place of numbers in your programs is always a good thing to do.  I use names for the coordinates of objects that I draw in TurtleSpace all the time, like buttons in the user interface part of a program.  This allows me to change them in one spot instead of searching for where the object is drawn, where I test to see if the mouse-click was within its bounds, etc...

Many computer languages have explicit support for global variables that, once assigned a value, can not be changed. 

Project: A Four-Function Calculator

Here is a Java applet that mimics the program you are going to write.

alt="Your browser understands the <APPLET> tag but isn't running the applet, for some reason." Your browser is completely ignoring the <APPLET> tag! Calculator Applet

Play around with it a bit, to see what it does when you click on its components.  Try adding two numbers, subtracting one number from another, etc...

A Four-Function Calculator:
How It Works

Figure 15.1

Figure 15.1 shows the calculator we're going to build.  It has space for 16 keys and a display.  There are ten digit keys used to enter numbers and five operation keys which determine what the calculator does.

As the mouse is clicked on number keys, the current value being accumulated and displayed is multiplied by 10 and the key's value is added in.  As an example, when the program starts, the current value is zero and when a number key is clicked on, the current value becomes the value of the key.  Let's say the "1" key is clicked on and the current value becomes 1.  If the mouse is then clicked on another number key, say "2," the new current value becomes 12 ( 1 * 10 + 2 ).  If the mouse is then clicked on the "3," the current value becomes 123 ( 12 * 10 + 3 ).

Figure 15.2

Figure 15.2 shows our calculator after a user has clicked on the "1" key, the "2" key, the "3" key, the "4" key, the "5" key, and the "6" key. 

Next we have the action keys.  The action keys: "/," "X," "-" and "+" do two things.

  1. They signal that entry of a number is complete.  The next number key that is clicked on becomes the new current number.
  2. The mathematical operation must be saved.  After another number is entered and the mouse is clicked on the "=" action key, the remembered operation is performed on the previous number and the current number and the result is displayed.

Continuing the example, Figure 15.3 shows our calculator after the user has clicked on the subtraction key ("-") and then on the "4" key, the "5" key, the "6" key, the "7" key, the "8" key, and the "9" key.

Figure 15.3

And, finally, Figure 15.4 shows our calculator after the user has clicked on the compute-answer key ("=").

Figure 15.4

A Four-Function Calculator:
Program Design

Let's think about the calculator as if it were a machine with a bunch of little people in it.  Take a few moments to think about how many you think would be needed and what each would do.  Don't continue reading until you have.

There is no single correct answer.  If you think you have a good team organization then I think you should go off and write you're version of the program.  You can always come back to check out my design when you are done, just to compare solutions.  Or, if at any point you get stuck, come back to read and get ideas.

I'm going to hire, train, and organize four little people.

  • One of my little people (Diva Display) will maintain the display area on our machine.  She just waits for someone to tell her there is a new number in the current number container.  When this happens she gets the number and draws it.
  • A second little person (Diego Digit) will handle all the digit keys, the 0 - 9 keys.  He will be told which of the digits was clicked on.  He just appends the new digit onto the right side of the number in the current number container.  Each time he puts a new number into the current number container, he sends a message to Diva so she knows she must display it.
  • Another little person (Omar Operations) makes decisions and shuffles things around.  He will be told which operation was requested - add, divide, equals, multiply, or subtract.  He will examine the contents of various containers, make a decision about what needs done, and maybe get Mary to compute something.  He always puts a new code into the math operator container, an indicator of any outstanding operation that needs performed.  In most cases, the number in current number is shuffled over into the previous number container.
  • Lastly, Mary Math will handle all of the adding, subtracting, etc....  She's behind the scenes, a real computer.  Whenever requested, Mary gets the numbers in the previous number and the current number containers, the operation in the math operation container, computes the answer and puts it into the current number container.  Since she changes the current number, she sends a message to Diva so the new current number can be drawn on the display.

Well, that's the way I can imagine putting together a machine with little people in it working together to provide the functionality of a simple, four-function calculator.

A Four-Function Calculator:
Program Structure

To reduce the time it will take you to write the calculator program, I'm going to provide you with most of my version of the program and the details of its structure.

I'm doing this because I want you to concentrate on learning about how/why global variables are used in programs - not how to design a calculator.  Since you are still learning the basics of programming, I want to offer you one way of structuring the program that I know will work.  How to design/structure a program on your own will be covered later.

Figure 15.5 shows the call graph for the procedures that make up my initial design of the calculator program.  The arrows indicate invocations of procedures.  Like always, the program is started by invoking the main procedure.  After this, all execution is driven by mouseClicked events (invocations of the procedure mouseClicked).

So here's a question for you...  Can you identify which groups of procedures, which parts of the pair of trees in Figure 15.5 are our little people?  Which procedures implement Diva, Diego, Mary, and Omar?  Take a little time to write down your thoughts.

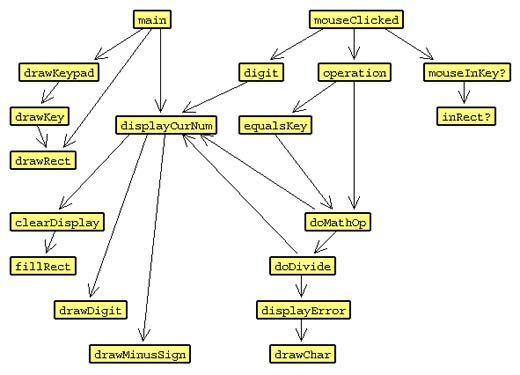Figure 15.5

Looking at Figure 15.5, you see that my calculator program consists of many procedures which you are already familiar with.  You've seen or written procedures: drawRect, fillRect, and inRect?. 

mouseInKey? is just a derivative of the mouseInRect? that you've written in the past - tuned for this program.  Since all the calculator's keys are the same sized squares, mouseInKey? does not need width and height inputs.

I'm going to give you most of my code for the calculator so that we can spend our time on the interesting procedures.  I'm including stubs (empty procedures) for these procedures.  Copy & paste the code (the following link gets you to) into the TG application.

Here is most of my calculator program, as a starting point..

Read the Code You've Been Given

The first thing you probably should do is read the code you now have.  In software development, modifying existing programs is what new hires most often get to do when they start.  Scanning over the existing code is important for at least two reasons:

  1. You need to see what you already have.  The last thing you want to do is go to the trouble of writing your own version of some procedure that already exists and is working.
  2. The best way to get good at programming is to read a lot of code - to see different ways to do stuff.

Once you have copied the source code into TG you can use the interactive environment it provides to help you understand what you've got.  One of the ways to understand the source code is to look at connections.

What do I mean by connections?

Well, the first half of the source code I've given you is a bunch of symbolic constants.  Checkout how each is used. 

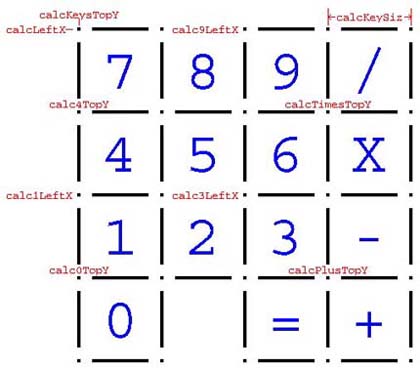
You can do this with the Editor's search command.  Click the mouse in TG's Editor and position the cursor at the top of the program.  Type [Ctrl]-s to get to the "Search for string:" prompt.  Type in calc3LeftX.  This should get you to the definition of its symbolic constant, its to calc3LeftX line.  You do not need to be CASE-specific.

Now type [Ctrl]-s [Ctrl]-s (typing [Ctrl]-s twice in close succession) which will get you to the next occurance of calc3LeftX.  It's used as an input to drawKey in the drawKeypad procedure.  This is the left edge of where drawKey draws a key.  Type [Ctrl]-s [Ctrl]-s again.  The next occurance is in the mouseclicked procedure.  It's used as an input to mouseInKey?, and again it is the leftmost edge of a rectangle (a calc key) that is being checked for a mouse click within its bounds. 

Using the search capability in the Editor helps you to see what things are used for.  And, this will give you a feeling for how you can use what has been provided. 

Figure 15.6 shows the layout of the keypad part of the calculator with a few points labeled with the names of the symbolic constants provided in the code I've given you.  Use the search capability in TG's Editor to find the occurances of these symbolic constants and discover how they are used.

Figure 15.6

Now, let's play around a bit.  Use the Interpret -> Editor Contents menu item to execute the program.  The calculator should be drawn, although there is no number in the display area.  Why?  main invokes drawRect to draw the outline of the calculator and then invokes drawKeypad which draws all the keys.  This behavior matches what you see in the program structure in (Figure 15.5). 

But, main doesn't invoke displayCurNum, which is probably why there is nothing in the display. You could invoke displayCurNum yourself in the CommandCenter.  Do it!  Nothing happens.  Reading the source code, you'll find that it's empty - you will need to fill it in. 

Above the definition of displayCurNum in the source code are some other procedure definitions with interesting names, e.g., clearDisplay, drawMinusSign, drawDigit, etc... Try invoking them in the CommandCenter.

You must provide drawDigit with two inputs.  The first is the X coordinate for where to draw the digit.  This should be one of the symbolic constants: calcDisp1sX, calcDisp10sX, etc... These symbolic constants are the X coordinates of the digit locations in the display, i.e., the ones column, the tens column, the hundreds column, etc...

Figure 15.7 shows the layout of the display part of the calculator with a few points labeled with the names of the symbolic constants provided in the code I've given you.

Figure 15.7

Exercise: Display Some Numbers

Use the CommandCenter to display a few different numbers.  Type in invocations of clearDisplay and then drawDigit to display numbers, say the powers of two which are four digits: 2048, 4096, and 8192.

A Four-Function Calculator:
Display Current Number

Okay, let's get going.  The first thing we will do is to get our calculator to display a current number.  Now we need a global variable.  The concept of a current number is a real need for one.  It's value will change as the user clicks on digit keys and the equals key.

In the source code I gave you, I included declarations for the global variables needed in the program.  I named the current number variable curNum.  The following lines are near the top of the source code. 

   ; the number displayed - just computed or being entered   
   global "curNum

But remember, declaring a global variable does not give it a value.  We need to add a make instruction to the program's main procedure to initialize this variable.  When you power up a calculator it's common for it to start off with the number zero.  Let's add the following instruction to main in our program. 

   make "curNum 0   

Now, every time that we change the value of curNum, we need to display the new value.  Look back at Figure 15.5 (the structure of the program).  It shows that main invokes displayCurNum.  Let's replace the comment line 

   ; ** display the current number - zero      **   

in main with an invocation of displayCurNum.  Here is our new main. 

   to main
     home clean hideturtle
     setlabelheight chLabelHeight
     setpencolor black setpensize 5
     drawRect calcLeftX calcTopY calcWidth calcHeight   
     drawKeypad
     make "curNum 0
     displayCurNum
     ; ** initialize all of the global variables **
     end

Now look back at the definition of displayCurNum.  OH, that's right, as we discovered a bit ago, displayCurNum doesn't do anything yet.  I guess it's time to fill in its body.  What does it need to do? 

It is the embodiment of Diva Display.  Her purpose is to keep the display on the calculator machine up to date.  Invoking the displayCurNum procedure in our program is just like telling Diva to get the contents of the current number container and draw it in the display area.  Think of invoking displayCurNum as sending Diva a message for her to act on.

As with most programming tasks, there are many different ways to draw the digits representing the value in the curNum variable.  Your job is to explore your own ideas.  I'm going to coach you through the way I approached the problem.  You should only continue reading if you really need to.

OK, what to do?  Where do we start?

Well, if you look back at Figure 15.5 (the structure of my program) you'll see that my displayCurNum only invokes three procedures: clearDisplay, drawDigit, and drawMinusSign.  Think about how to display the value in curNum.  It's not too hard to see why and how we can use two of the three. 

   to displayCurNum
     clearDisplay
     if less? :curNum 0 [drawMinusSign]
     ;draw digits representation of :curNum   
     end

Before we draw anything in the display, we need to erase anything that's already there.  And then, if the value in curNum is less than zero we should invoke drawMinusSign. Now we are left with how to use drawDigit.  Obviously, it needs to be invoked once for each digit that we need to draw, but how do we isolate each of them?

Some Math Lessons

I always like to approach a programming problem by thinking, asking myself, "How can I get just a piece of the problem solved, and then worry about what remains once I've accomplished this?"

So, let's just concentrate on getting the rightmost column displayed for now.  Let's invoke drawDigit for the ones column, regardless of what the contents of curNum is.

So, how do we isolate the rightmost digit?  What mathematical operation will get us the ones column, no matter how big the number in curNum is?  What will get us a "1" when curNum contains 1, or 21, 321, or 4321, or any number ending with a one?

What about the remainder left over when curNum is divided by ten (10)?  Divide one by ten and you get zero, with a remainder of one.  Divide twenty-one by ten and you get two, with a remainder of one.  I don't think I need to give any more examples... 

Time to use TG's HELP directive to see what numeric operations are available.  If you forget the organization of TG's HELP stuff, just type the word "help" in the CommandCenter.  The response shows that you can ask for help on a category and there is a category with the name "NumOpr" which is short for NUMber OPeRations.  So, in our case, you type "help numopr" into the CommandCenter.

And... yes, Logo has a REMAINDER operator.

Name Input(s) Description
 REMAINDER   number1  number2  Outputs the remainder left after dividing number1 by number2

Here's our new displayCurNum procedure. 

   to displayCurNum
     clearDisplay
     if less? :curNum 0 [drawMinusSign]
     ;draw digits of :curNum (greater than ones-column)   
     drawDigit calcDisp1sX remainder :curNum 10
     end

Try out displayCurNum.  Put a few different values into curNum with the make command.  Then invoke displayCurNum and see what happens.

Well, I found a bug.  Did you try putting a negative number into curNum?  I did and Figure 15.8 shows what I saw.

Figure 15.8

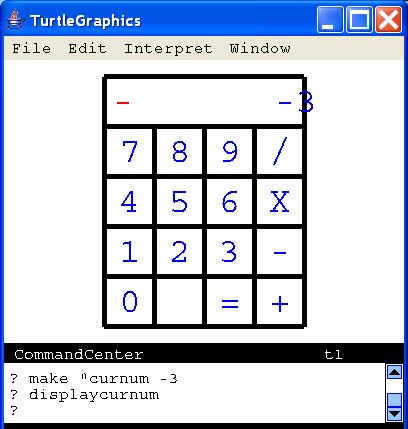Oh well, it looks like we need to use the absolute value of curNum when we are drawing the digits.  Does Logo have an operator that provides the absolute value of an input?

Check for one like you did above for a remainder operation.

And... Yes, Logo has an operator which outputs the absolute value of its input.

Name Input(s) Description
 ABS   number  Outputs the absolute value of number

But, we can't change curNum - it needs to stay negative.  We need to modify our procedure to use a local variable, a copy of curNum which displayCurNum can feel free to change.  Here is my new, improved version of displayCurNum. 

   to displayCurNum
     clearDisplay
     if less? :num 0 [drawMinusSign]
     localmake "num abs :curNum
     ;draw digits of :num (greater than ones-column)   
     drawDigit calcDisp1sX remainder :num 10
     end

Other than the use of ABS, the changes just reflect the addition of a local variable (num), which you learned all about in the previous lesson.  In displayCurNum, the local variable num will hold the absolute value of curNum.  This will eliminate the problem of label prefixing a minus sign to the digits we want to draw.

Finally, what is left to do is add code to handle drawing the other digits, the digit in the tens column, the digit in the hundreds column, etc...  Again, there are a couple of different ways to isolate each digit.

Try to complete the displayCurNum before reading on.  Take it one column at a time; answer the question: "How can I isolate and display the tens-column's digit?"  Play around a bit in the CommandCenter.  Try to isolate the tens digit.  Do this BEFORE you continue reading.

Hopefully you discovered that combining the remainder operator with the quotient operator almost got you what you wanted.  The glitch is that division produces numbers with fractions, e.g., quotient 4321 10 outputs 432.1.  If we use this as the first input to remainder, and "10" as its second input, we will not get an isolated 2.  Time to use HELP again... We need a numeric operator that removes the fractional part.

Example: Display the isolated digits of the number 4321 

   println remainder (int quotient 4321 1000) 10    
   println remainder (int quotient 4321 100) 10
   println remainder (int quotient 4321 10) 10
   println remainder 4321 10

Use the CommandCenter in the TG program you're using or go back up to the TG Applet and type in the above example.  Play around a bit until you see/understand what is going on...

Add code to your displayCurNum procedure to draw the additional columns.  Then, try it out.  Put a few different numbers into curNum with make and then invoke displayCurNum.

Well, we are almost done.  But, it looks like we have a bug to fix first.  We need to eliminate the display of leading zeroes.  Figure 15.9 shows what I'm pretty sure you see if you put 4321 into curNum.

Figure 15.9

Before you draw each digit, you must first determine whether or not it needs to be drawn.  As an example, unless :num is greater than nine (9), all you need to draw is the rightmost digit, the ones-column digit.  But, if :num is greater than nine then you know that you need to draw a digit in the tens-column.  If :num is greater than ninety-nine (99) then you need to draw a digit in the hundreds column. Etc...

How do you control whether some code gets performed?  With an if command of course...  Here is an example of an if instruction that may help. 

  if greater? :num 9 [drawDigit calcDisp10sX <isolated-tens-digit>]  

You can complete the if instruction given above by exchanging the isolated-tens-digit piece with code that does just that...

OK... I've given you enough hints.  It's up to you to complete your displayCurNum procedure.  When you complete it, test it out. 

A Four-Function Calculator:
Mouseclick on a Number Key

Ok, we have the display working.  Let's move on to entering a full number, the embodiment of Diego Digit.

In the code I've given you, look at the mouseClicked procedure.  Here is a snipet of it. 

   to mouseClicked
     if mouseInKey? calc0LeftX  calc0TopY [digit 0 stop]   
     if mouseInKey? calc1LeftX  calc1TopY [digit 1 stop]
     ...

The digit procedure is invoked in the mouseClicked procedure when the user clicks on any of the digit keys.  The number value of the digit key clicked on is provided as the input to digit.:  So, what does digit need to do?

It must do what I said Diego Digit would be doing.  Read the description of what he does again just to refresh your memory.

The digit procedure has one input, the number for the key just clicked on.  This number gets appended (becomes the new least significant digit of) to the number in the current number container, curNum.  You simply multiply the current number by 10 and add in the new digit.

Oh... there's one more thing that digit needs to do.  I'll let you figure it out.  The description of what Diego Digit does contains a clue.  And take a look at Figure 15.5 (the program structure) if you need another clue.

Once you have the body of digit filled in, test it out.  You should be able to invoke main in the CommandCenter and then click on digits and watch the number change in the calculator's display.

A Four-Function Calculator:
The Operation Keys

Ok, on to the rest of the keys on our calculator; what do they need to do?

They must do what I said Omar Operations would be doing.  Read the description of what he does again, just to refresh your memory.

The operation keys signal a few things.

  1. The current number is complete.  Our calculator program now has at least the first of two numbers that it will use in a calculation.  We need to save it somewhere and prepare for a new current number.
  2. For the math operation keys, we know what operation to perform when the next operation key is clicked on.  This bit of information must be saved.
  3. For the equals key, it's time to perform the last requested math operation.

So, a lot of what needs done is at the root of this lesson on global variables.  Information that has been gathered (the current number) and which operation key was clicked on must be saved for future use.  Since it is in the future, from the perspective of our running program, the data must go into global variables.

At this point when I was writing my version of the calculator, I added two more global variables.  I created a prevNum variable which I wanted to hold the previous number and a mathOp variable to hold the chosen mathematical operation.  Again, since global variable declarations do not include a way to initialize them (put initial values into the variable), I needed to add make commands to do this in main.  I gave you the global declarations but not the code in main so you'll have to add this yourself.

The Operation Keys - The Divide, Minus, Plus, and Times Keys

My first pass at the operation keys was to write a procedure for each key.  I had divideKey, equalsKey, minusKey, plusKey, and timesKey procedures.  When I was done, I noticed that all of the procedures except equalsKey did the same thing.

As an example, my plusKey procedure set prevNum to the value in curNum (the current number).  Then it put zero into curNum.  Finally, it put the word add into mathOp.

The other math operation keys did the same except for the value of the word stored into mathOp - each was different.  Sounds like an opportunity to use an input variable to me!

So, I renamed one of the math operation procedures to be operation and gave it an input that would be for the operation code (opcode) that gets put into mathOp.  Then I deleted the three remaining math operation procedures.

What about the equals key?.  Remember that I said it was the exception? 

Well... The first instruction in in my operation procedure is an IF command that checks if its input opcode contains "eql.  If so, the equalsKey procedure is invoked and then it STOPs, i.e., leaves operation.

Enough coaching...  Time for you to fill in the code for the operation procedure.

The Operation Keys - Testing What You've Done

Until operation, it was easy to tell whether the code we were writing was working or not.  Everything we did resulted in changes on the calculator's display.  But, for the code we've just added, there is no way to see that the program is doing what we want.  OR, is there?

One way to see what our program is doing is to use trace like I've recommended for debugging.  Similar to the way procedure execution can be traced, global variables can be traced.  Figure 15.10 shows results of my tracing curNum and mathOp.

Figure 15.10

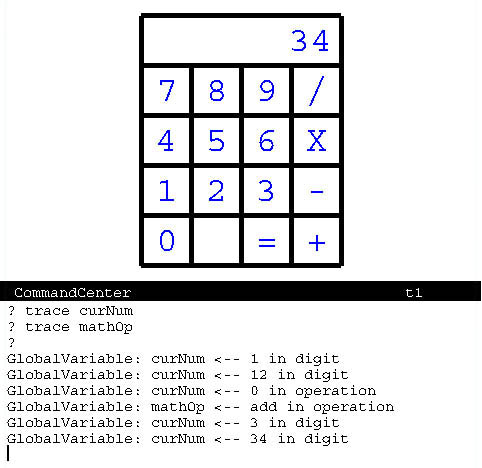After entering the two trace directives ("trace curNum" and "trace mathOp") into the CommandCenter, I then clicked on

  • the "1" key,
  • the "2" key,
  • the "+" key,
  • the "3" key, and
  • the "4" key.

As you can see in Figure 15.10, the global variable's identifier is printed followed by the value that is being put into it and the current procedure.

Sometimes using trace generates too much output in the CommandCenter.  Another common way to see if your programs are doing what you think is to add println commands.  In our case, before we write the body of equalsKey we can add a single println command to print out the contents of all of our global variables.  Here's an example.  First I added my println command to my empty equalsKey. 

   to equalsKey
     println se "curNum= se :curNum se "prevNum= se :prevNum se "mathOp= :mathOp   
     end

Next I chose the "Interpret->Editor Contents" menu item and then clicked on

  • the "7" key,
  • the "8" key,
  • the "-" key,
  • the "3" key,
  • the "2" key, and
  • the "=" key.

The result was 

   curNum= 32 prevNum= 78 mathOp= sub  

printed in the CommandCenter.  And this shows us that all of the global variables contain exactly what expected.  We're ready to move on to writing the body of equalsKey.

The Operation Keys - The Equals Key

But, what does the equalsKey do?  A mouse click on the equals key signals two things.

  1. the current number is complete.  The calculator probably now has the second number that is required for generating an answer.
  2. it's time to perform the saved math operation and display the answer.

Back in the description of what Omar Operations does it mentions that he shuffles things around, makes decision about what to do, and he might "get Mary to compute something."  Well, operations has decided the equals key was clicked on and invoked equalsKey.  If there ever was a time to compute something, it's now.  But where in our program is Mary Math? 

Read through the program to see if you can find her.  See if you can find her in Figure 15.5.  The way a request is made is by invoking a procedure.  But, what is the name of the procedure that equalsKey needs to invoke to get a math operation performed?

There is one more thing that equalsKey must do.  After the math has been performed, it is important to note this.  Where are we keeping track of outstanding math operations?  Answer: in the mathOp global variable.  So, once Mary has completed the math operation, we had better put the word "nop into the mathOp container.  So, here is our finished equalsKey. 

   to equalsKey
     ;get Mary Math to do the expected computation    
     make "mathOp "nop
     end

Ok, complete this procedure before moving on in the lesson.

A Four-Function Calculator:
Mary Math, the Computer

This is it, the last code we need to write to get our calculator working.

Read the description of what Mary Math does again, just to refresh your memory.

The description is so good that you should be able to write the body for doMathOp on your own.  No need for coaching here...

Bugs

Removing the Fractional Part

To reduce the complexity of you first version of the calculator, it does not support a fractional part.  So, you need to know how to get rid of it before you attempt to display a number.  Even though the user can not enter a number with a fractional part, one can be generated with division, e.g., divide 100 by 3.  The round operator takes one input and outputs the closest integer to it.  The first thing that displayCurNum needs to do is make sure that curNum is an integer.

What's Special About Division

You may not have noticed when you were writing the body of doMathOp, but right above it in the code I provided is an empty procedure named doDivide.  Why do you think I had to write a special procedure just to handle division?  Checkout in Figure 15.5 to see who invokes it.  Sure enough - it gets invoked by doMathOp.  But... WHY?  Notice that doDivide invokes displayError!  There's another clue. 

Think about a special check you need to make when you are performing division.  When you have it, fill in the body of doDivide and invoke it in doMathOp.

Practice: Some Extensions You Can Make

Now that you have your basic calculator working, extend it a bit.  Here are some ideas for you to explore.  But, the sky is the limit; come up with your own additions too.

  1. When multiple math operations need to performed consecutively, there should be no need to click on the equals key after the second number is entered.  In other words, you should be able to add a list of numbers as follows.
    • Enter the first number, say 123,
    • click on the "+" key,
    • enter the second number, say 456,
    • click on the "+" key,
    • enter the third number, say 789,
    • and then finally click on the "=" key.
  2. Add a "CLEAR" key to your calculator.  It should zero out the current and previous numbers, and the display.
  3. Add little icons somewhere on the display of your calculator to show what mathematical operation is about to be performed.

Summary

Global variables are containers that are created with the global command and can be accessed anywhere in your program.  One gotcha is that the global command that introduces the variable (called its declaration) must be interpreted before its identifier can be entered in an instruction.  But a nice habit to get into is to put all of your global declarations at the top of your program.  If you do this, you are guaranteed the declarations always preceed the use of the variables.

Most introductory programming classes/texts introduce global variables much sooner than I have.  I've worked on lots and lots of code in my days as a programmer and I've seen too many inappropriate uses of global variables.  Their usage (I guess I should say their misuse) is a common source of bugs.  Global variables are a very important, powerful concept in programming.  But, use them responsibly.

To read more about trouble you can get into with global variables, Google "global variables considered harmful" and check out the pages that come up.  William Wulf and Mary Shaw wrote a paper a long time ago that is still referenced/debated today.

Back to Local Variables
Go to the Table of Contents
On to Word & Sentence Iteration

Public Domain Mark
This work (BFOIT: Introduction to Computer Programming, by Guy M. Haas),
identified by Berkeley Foundation for Opportunities in IT (BFOIT),
is free of known copyright restrictions.