BFOIT ICSI

Background

jLogo Programming

Java

Appendices

Updates

Lastly

Computer Science Logo Style, Volume 1, Chapter 7

Introduction to Recursion

Brian Harvey
University of California, Berkeley

NOTE: This webpage contains a slightly modified version of Brian Harvey's chapter. I have made minor changes, primarily in the examples, so that the code works with the TG applet/application and fits in with the rest of the BFOIT material. Here is Brian's original text. -- guy

My goal in this chapter is to write a procedure named downup that behaves like this:

? downup "hello
hello
hell
hel
he
h
he
hel
hell
hello
? downup "goodbye
goodbye
goodby
goodb
good
goo
go
g
go
goo
good
goodb
goodby
goodbye

The programming techniques we've used so far in this book don't allow an elegant solution to this problem. We'll use a new technique called recursion: writing a procedure that uses itself as a subprocedure.

We're going to solve this problem using recursion. It turns out that the idea of recursion is both very powerful--we can solve a lot of problems using it--and rather tricky to understand. That's why I'm going to explain recursion several different ways in the coming chapters. Even after you understand one of them, you'll probably find that thinking about recursion from another point of view enriches your ability to use this idea. The explanation in this chapter is based on the combining method.

Starting Small

My own favorite way to understand recursion is based on the general problem-solving strategy of solving a complicated problem by starting with a simpler version. To solve the downup problem, I'll start by solving this simpler version: write a downup procedure that works only for a single-character input word. (You can't get much simpler than that!) Here's my solution:

to downup1 :word
  println :word
  end

? downup1 "j
j

See how well it works?

Building Up

Of course, downup1 won't work at all if you give it an input longer than one character. You may not think this was such a big step. But bear with me. Next I'll write a procedure that acts like downup when you give it a two-letter input word:

to downup2 :word
  println :word
  println butlast :word
  println :word
  end

? downup2 "it
it
i
it

We could keep this up for longer and longer input words, but each procedure gets more and more complicated. Here's downup3:

to downup3 :word
  println :word
  println butlast :word
  println butlast butlast :word
  println butlast :word
  println :word
  end

- How many println instructions would I need to write downup4 this way? How many would I need for downup20?

Luckily there's an easier way. Look at the result of invoking downup3:

? downup3 "dot
dot

  
  do
  d
  do
  

dot

The trick is to recognize that the boxed lines are what we'd get by invoking downup2 with the word do as input. So we can find the instructions in downup3 that println those three lines and replace them with one instruction that calls downup2:

to downup3 :word
  println :word
  downup2 butlast :word
  println :word
  end

You might have to think a moment to work out where the butlast came from, but consider that we're given the word dot and we want the word do.

Once we've had this idea, it's easy to extend it to longer words:

to downup4 :word
  println :word
  downup3 butlast :word
  println :word
  end

to downup5 :word
  println :word
  downup4 butlast :word
  println :word
  end

- Can you rewrite downup2 so that it looks like these others?

- Before going on, make sure you really understand these procedures by answering these questions: What happens if you use one of these numbered versions of downup with an input that is too long? What if the input is too short?

Generalizing the Pattern

We're now in good shape as long as we want to downup short words. We can pick the right version of downup for the length of the word we have in mind:

? downup5 "hello
hello
hell
hel
he
h
he
hel
hell
hello
? downup7 "goodbye
goodbye
goodby
goodb
good
goo
go
g
go
goo
good
goodb
goodby
goodbye

Having to count the number of characters in the word is a little unaesthetic, but we could even have the computer do that for us:

to downup :word
  if equal? count :word 1 [downup1 :word]
  if equal? count :word 2 [downup2 :word]
  if equal? count :word 3 [downup3 :word]
  if equal? count :word 4 [downup4 :word]
  if equal? count :word 5 [downup5 :word]
  if equal? count :word 6 [downup6 :word]
  if equal? count :word 7 [downup7 :word]
  end

There's only one problem. What if we want to be able to say

downup "antidisestablishmentarianism

You wouldn't want to have to type in separate versions of downup all the way up to downup28!

What I hope you're tempted to do is to take advantage of the similarity of all the numbered downup procedures by combining them into a single procedure that looks like this:

to downup :word
  println :word
  downup butlast :word
  println :word
  end

Compare this version of downup with one of the numbered procedures like downup5. Do you see that this combined version should work just as well, if all the numbered downup procedures are identical except for the numbers in the procedure names? Convince yourself that that makes sense.

- Okay, now try it.

What Went Wrong?

You probably saw something like this:

? downup "hello
hello
hell
hel
he
h

followed by a pop-up ERROR: (downup) Can't do butlast on an empty word.

There's nothing wrong with the reasoning I used in the last section. If all the numbered downup procedures are identical except for the numbers, it should work to replace them all with a single procedure following the same pattern.

The trouble is that the numbered downup procedures aren't quite all identical. The exception is downup1. If it were like the others, it would look like this:

to downup1 :word
  println :word
  downup0 butlast :word
  println :word
  end

Review the way the numbered downups work to make sure you understand why downup1 is different. Here's what happens when you invoke one of the numbered versions:

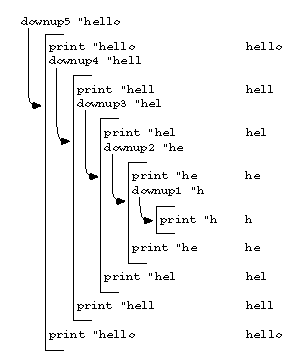
In this chart, instructions within a particular procedure are indented the same amount. For example, the lines println "hello and downup4 "hell are part of downup5, as is the line println "hello at the very end of the chart. The lines in between are indented more because they're part of downup4 and its subprocedures.

(By the way, the lines in the chart don't show actual instructions in the procedure definitions. Otherwise all the println lines would say println :word instead of showing actual words. In the chart I've already evaluated the inputs to the commands.)

The point of the chart is that downup1 has to be special because it marks the end of the "down" part of the problem and the beginning of the "up" part. downup1 doesn't invoke a lower-numbered downup subprocedure because there's no smaller piece of the word to println.

- Okay, Logo knows when to stop the "down" part of the program because downup1 is different from the other procedures. Question: How does Logo know when to stop the "up" part of the program? Why doesn't downup5, in this example, have to be written differently from the others?

The Stop Rule

Our attempt to write a completely general downup procedure has run into trouble because we have to distinguish two cases: the special case in which the input word contains only one character and the general case for longer input words. We can use ifelse to distinguish the two cases:

to downup :word
  end

to downupMany :word
  println :word
  downup butlast :word
  println :word
  end

to downupOne :word
  println :word
  end

to downup :word
  ifelse equal? count :word 1 [downupOne :word] [downupMany :word]
  end

You'll find that this version of the downup program actually works correctly. Subprocedure downupOne is exactly like the old downup1, while downupMany is like the version of downup that didn't work.

It's possible to use the same general idea, however -- distinguishing the special case of a one-letter word -- without having to set up this three-procedure structure. Instead we can take advantage of the fact that downupOne's single instruction is the same as the first instruction of downupMany; we can use a single procedure that stops early if appropriate.

to downup :word
  println :word
  if equal? count :word 1 [stop]
  downup butlast :word
  println :word
  end

The if instruction in this final version of downup is called a stop rule.

Downup illustrates the usual pattern of a recursive procedure. There are three kinds of instructions within its definition: (1) There are the ordinary instructions that carry out the work of the procedure for a particular value of the input, in this case the println instructions. (2) There is at least one recursive call, an instruction that invokes the same procedure with a smaller input. (3) There is a stop rule, which prevents the recursive invocation when the input is too small.

It's important to understand that the stop rule always comes before the recursive call or calls. One of the common mistakes made by programmers who are just learning about recursion is to think this way: "The stop rule ends the program, so it belongs at the end of the procedure." The right way to think about it is that the purpose of the stop rule is to stop the innermost invocation of the procedure before it has a chance to invoke itself recursively, so the stop rule must come before the recursive call.

Local Variables

When you're thinking about a recursive procedure, it's especially important to remember that each invocation of a procedure has its own local variables. It's possible to get confused about this because, of course, if a procedure invokes itself as a subprocedure, each invocation uses the same names for local variables. For example, each invocation of downup has a local variable (its input) named word. But each invocation has a separate input variable.

It's hard to talk about different invocations in the abstract. So let's look back at the version of the program in which each invocation had a different procedure name: downup1, downup2, and so on.

If you type the instruction

downup5 "hello

the procedure downup5 is invoked, with the word hello as its input. Downup5 has a local variable named word, which contains hello as its value. The first instruction in downup5 is

println :word

Since :word is hello, this instruction prints hello. The next instruction is

downup4 butlast :word

This instruction invokes procedure downup4 with the word hell (the butlast of hello) as input. Downup4 has a local variable that is also named word. The value of that variable is the word hell.

At this point there are two separate variables, both named word. Downup5's word contains hello; downup4's word contains hell. I won't go through all the details of how downup4 invokes downup3 and so on. But eventually downup4 finishes its task, and downup5 continues with its final instruction, which is

println :word

Even though different values have been assigned to variables named word in the interim, this variable named word (the one that is local to downup5) still has its original value, hello. So that's what's printed.

In the recursive version of the program exactly the same thing happens about local variables. It's a little harder to describe, because all the procedure invocations are invocations of the same procedure, downup. So I can't say things like "the variable word that belongs to downup4"; instead, you have to think about "the variable named word that belongs to the second invocation of downup." But even though there is only one procedure involved, there are still five procedure invocations, each with its own local variable named word.

More Examples

- Before I go on to show you another example of a recursive procedure, you might try to write down and up, which should work like this:

? down "hello
hello
hell
hel
he
h
? up "hello
h
he
hel
hell
hello

As a start, notice that there are two println instructions in downup and that one of them does the "down" half and the other does the "up" half. But you'll find that just eliminating one of the printlns for down and the other for up doesn't quite work.

After you've finished down and up, come back here for a discussion of a similar project, which I call inout:

? inout "hello
hello
 ello
  llo
   lo
    o
   lo
  llo
 ello
hello

At first glance inout looks just like downup, except that it uses the butfirst of its input instead of the butlast. Inout is somewhat more complicated than downup, however, because it has to print spaces before some of the words in order to line up the rightmost letters. Downup lined up the leftmost letters, which is easy.

Suppose we start, as we did for downup, with a version that only works for single-letter words:

to inout1 :word
  println :word
  end

But we can't quite use inout1 as a subprocedure of inout2, as we did in the downup problem. Instead we need a different version of inout1, which prints a space before its input:

to inout2.1 :word
  print "\                   ; quote, backslash, followed by a space
  println :word
  end

to inout2 :word
  println :word
  inout2.1 butfirst :word
  println :word
  end

Print is a command, which requires one input. The input can be any datum. Print prints its input, like println, but does not move the cursor to a new line afterward. The cursor remains right after the printed datum, so the next println or print command will continue on the same line.

We need another specific case or two before a general pattern will become apparent. Here is the version for three-letter words:

to inout3.1 :word
  repeat 2 [print "\ ]
  println :word
  end

to inout3.2 :word
  print "\ 
  println :word
  inout3.1 butfirst :word
  print "\ 
  println :word
  end

to inout3 :word
  println :word
  inout3.2 butfirst :word
  println :word
  end

Convince yourself that each of these procedures prints the right number of spaces before its input word.

Here is one final example, the version for four-letter words:

to inout4.1 :word
  repeat 3 [print "\ ]
  println :word
  end

  to inout4.2 :word
  repeat 2 [print "\ ]
  println :word
  inout4.1 butfirst :word
  repeat 2 [print "\ ]
  println :word
  end

to inout4.3 :word
  print "\ 
  println :word
  inout4.2 butfirst :word
  print "\ 
  println :word
  end

to inout4 :word
  println :word
  inout4.3 butfirst :word
  println :word
  end

- Try this out and try writing inout5 along the same lines.

How can we find a common pattern that will combine the elements of all these procedures? It will have to look something like this:

to inout :word
  repeat something [print "\ ]
  println :word
  if something [stop]
  inout butfirst :word
  repeat something [print "\ ]
  println :word
  end

This is not a finished procedure because we haven't figured out how to fill the blanks. First I should remark that the stop rule is where it is, after the first println, because that's how far the innermost procedures (inout2.1, inout3.1, and inout4.1) get. They print some spaces, print the input word, and that's all.

Another thing to remark is that the first input to the repeat commands in this general procedure will sometimes be zero, because the outermost procedures (inout2, inout3, and inout4) don't print any spaces at all. Each subprocedure prints one more space than its superprocedure. For example, inout4 prints no spaces. Its subprocedure inout4.3 prints one space. inout4.3's subprocedure inout4.2 prints two spaces. Finally, inout4.2's subprocedure inout4.1 prints three spaces.

In order to vary the number of spaces in this way, the solution is to use another input that will have this number as its value. We can call it spaces. The procedure will then look like this:

to inout :word :spaces
  repeat :spaces [print "\ ]
  println :word
  if equal? count :word 1 [stop]
  inout (butfirst :word) (sum :spaces 1)
  repeat :spaces [print "\ ]
  println :word
  end

? inout "hello 0
hello
 ello
  llo
   lo
    o
   lo
  llo
 ello
hello

Notice that, when we use inout, we have to give it a zero as its second input. We could eliminate this annoyance by writing a new inout that invokes this one as a subprocedure:

to inoutHelper :word :spaces
  repeat :spaces [print "\ ]
  println :word
  if equal? count :word 1 [stop]
  inoutHelper (butfirst :word) (sum :spaces 1)
  repeat :spaces [print "\ ]
  println :word
  end

to inout :word
  inoutHelper :word 0
  end

(The easiest way to make this change is to edit inout with the editor and change its title line and its recursive call so that its name is inoutHelper. Then, type in the new superprocedure inout.)

This program structure, with a short superprocedure and a recursive subprocedure, is very common. The superprocedure's only job is to provide the initial values for some of the subprocedure's inputs, so it's sometimes called an initialization procedure. In this program inout is an initialization procedure for inoutHelper.

By the way, the parentheses in the recursive call aren't really needed; I just used them to make it more obvious which input is which.

Other Stop Rules

The examples I've shown so far use this stop rule:

if equal? count :word 1 [stop]

Perhaps you wrote your down procedure the same way:

to down :word
  println :word
  if equal? count :word 1 [stop]
  down butlast :word
  end

Here is another way to write down, which has the same effect. But this is a more commonly used style:

to down :word
  if empty? :word [stop]
  println :word
  down butlast :word
  end

This version of down has the stop rule as its first instruction. After that comes the instructions that carry out the specific work of the procedure, in this case the println instruction. The recursive call comes as the last instruction.

A procedure in which the recursive call is the last instruction is called tail recursive. We'll have more to say later about the meaning of tail recursion. (Actually, to be precise, I should have said that a command in which the recursive call is the last instruction is tail recursive. What constitutes a tail recursive operation is a little tricker, and so far we haven't talked about recursive operations at all.)

Here's another example:

to countdown :number
  if equal? :number 0 [println "Blastoff! stop]
  println :number
  countdown difference :number 1
  end

? countdown 10
10
9
8
7
6
5
4
3
2
1
Blastoff!

In this case, instead of a word that gets smaller by butfirsting or butlasting it, the input is a number from which 1 is subtracted for each recursive invocation. This example also shows how some special action (the println "Blastoff! instruction) can be taken in the innermost invocation of the procedure.

- Here are some ideas for recursive programs you can write. In each case I'll show an example or two of what the program should do. Start with printPiecePerLine, a command with one input. If the input is a word, the procedure should print each letter of the word on a separate line. If the input is a list, the procedure should print each member of the list on a separate line:

? printPiecePerLine "hello
h
e
l
l
o
? printPiecePerLine [the rain in spain]
the
rain
in
spain

- As an example in which an initialization procedure will be helpful, try triangle, a command that takes a word as its single input. It prints the word repeatedly on the same line, as many times as its length. Then it prints a second line with one fewer repetition, and so on until it prints the word just once:

? triangle "frog
frog frog frog frog
frog frog frog
frog frog
frog

- A more ambitious project is diamond, which takes as its input a word with an odd number of letters. It displays the word in a diamond pattern, like this:

? diamond "program
   g
  ogr
 rogra
program
 rogra
  ogr
   g

(Hint: Write two procedures diamondTop and diamondBottom for the growing and shrinking halves of the display. As in inout, you'll need an input to count the number of spaces by which to indent each line.) Can you write diamond so that it does something sensible for an input word with an even number of letters?

Brian Harvey, bh@cs.berkeley.edu